Next, turn the objects and the paper slightly, as in Figure 38, but do not change the position of the frame. Repeat the tracing process. The retreating lines of the long sides will now converge to a point somewhere outside and to the right of the frame. The short lines of the objects, which in Figure 37 are horizontal, now converge to a distant point at the left. If the frame were wide enough, both sets of lines would be seen to come to points on the same horizontal line—the eye-level—demonstrating two-point perspective.
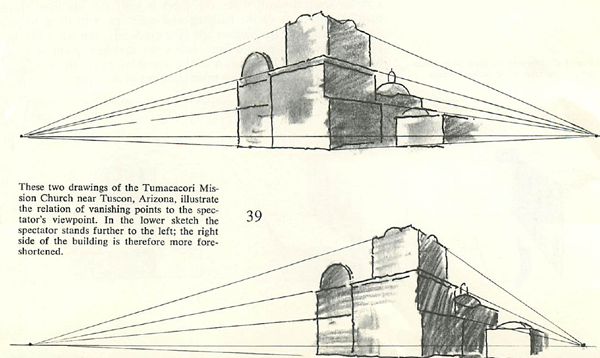
This is further shown in the drawings of the mission [Figure 39].
We have a rule here: all horizontal, parallel, retreating lines converge to the same point on the eye-level, which is also the horizon line. Where that point is depends upon the angle at which the objects are placed in relation to the picture plane. Referring again to the drawing of “The Old Mission,” it is seen that the vanishing point of the lines on the greatly foreshortened face of the building—the right side—is closer to the structure than the vanishing point of the lines of the less-foreshortened side. The nearer the spectator is to the building the more acute the angle of convergence at its corner, and the closer the vanishing points. At greater distances the less acute the angle of convergence and the farther removed the vanishing points. If a tracing is made of “The Old Mission,” except that the vanishing points are carried out seven or eight inches farther on both sides, the effect will be as though the spectator had gone back perhaps a hundred yards to view the structure. Should the vanishing points be extended as much as thirty inches farther, the building would be pushed into the far distance and the convergence of the lines would be scarcely noticeable. Try these experiments.
The important fact to remember is that the tipping of the street plane does not affect the perspective of the building lines; an obvious enough truth, yet a frequent point of confusion for beginners.
In order to reproduce the true effect of a street on such an incline, the heights of the three house-units in our model have been adjusted (c) at intervals to conform to the circumstances.
In Figure 43 are photographs of a barn on an inclined road. One picture was made from below, another from above. So in the former the eye-level (dotted line) is low on the building. In the latter it is higher, coinciding with the clapboards which, in the print, are horizontal at that point. The vanishing points of the building’s short lines are at too great a distance to permit showing them on the page.
The drawing of a street in an English hill town [Figure 44 illustrates the perspective facts when the spectator is standing in the street looking up. In such a situation there are two vanishing points as demonstrated in the accompanying line analysis. The horizontal building lines always converge to the same point at the eye-level (dotted line). The street lines here converge to a higher point because we are looking up the hill. The inclination of the street will be most evident in a drawing when horizontal building lines are given as much emphasis as possible in order to contrast with the inclined street lines.
Click on Link Below to Go to the Next Page





Very good webiste. This is very helpful for all seo. Thanks!
execellent