DRAWING & SHADING SPHERES, CIRCLES, AND ELLIPSES : How to Draw Lights and Shade Shadows of Spheres & Balls

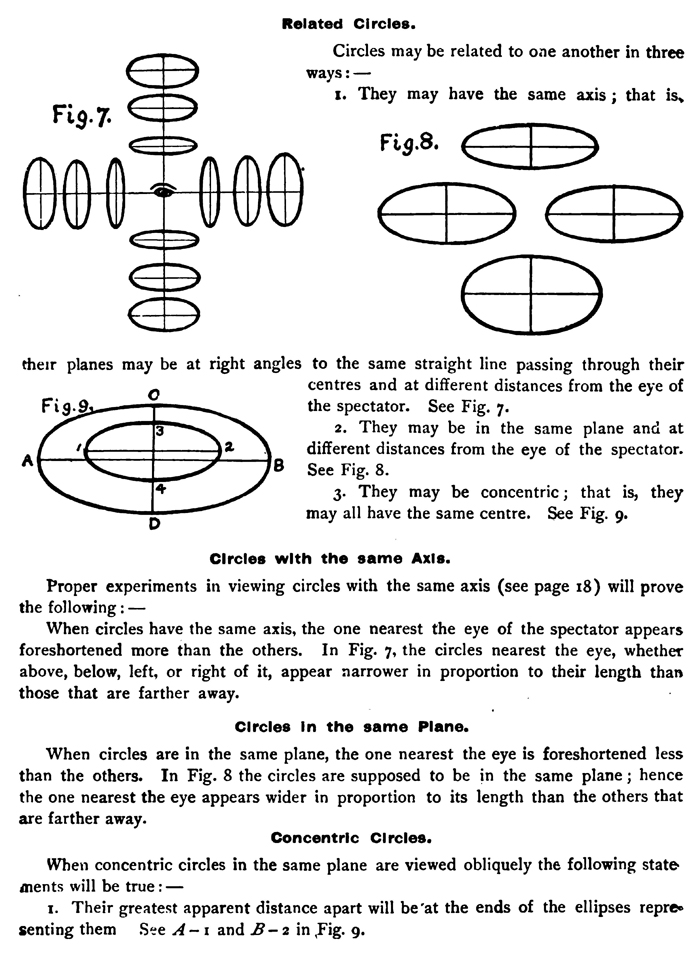
The above text is actually made up of images....so if you need to copy some text, you can do so below. Thanks.

Drawing The Sphere.

The sphere being the most symmetrical of all objects, the simplest of the bodies circular in section, and without appreciable foreshortening in its apparent outline, is take:, as the beginning point of a practical course in object drawing.

A sphere is a solid, bounded by an evenly curved surface, every point of which is equally distant from a point within, called its center.

In every possible position and at every visible distance, the sphere appears so nearly circular that its outline must always be represented as the circumference of a perfect:

circle. This is the only object in which no possible foreshortening can take place in the drawing of its outline. Objects similar to a sphere may be slightly foreshortened in their outlines, depending on the relative position to the eye of the observer.

The Plane Circle.

The second object to be drawn is a right cylinder ; but as each end of such a cylinder is a plane circle it is perhaps better to learn to draw a plane circle first.

A circle is a plane figure, every point of whose outline, called its circumference, is equally distant from a point within, called its center.

When the plane of the circle is at right angles to the line of direction, it will not appear to be foreshortened in any direction ; hence it must appear of its real shape, that is, as the circumference of a perfect circle.

When the plane of the circle makes an angle with the line of direction different from a right angle, it will be foreshortened in thickness, or from the nearest point to the farthest point, but not in the direction at right angles to this last direction ; hence it will appear as the circumference of what may be termed in ordinary language a flattened circle, but which we technically call an ellipse.

When the plane of the circle contains the line of direction, the apparent width from the nearest point to the farthest point will be reduced by foreshortening to nothing ; hence the circle will appear as a straight line.

The above forms, the perfect circle, the ellipse, and the straight line, are the only appearances a plane circle can have when viewed at some distance and when the line of direction is toward the central part of the circle.

When circles are comparatively large, and the spectator is on or within the circumference and is looking beyond the circle, or is so situated as to take into the field of vision only the farther part of the circle, such part of the circle may have the appearance of a parabola or an hyperbola ; but these cases are so rare that they need not be dwelt upon in elementary model drawing.

When well understood, by abundant illustration and the performance of many experiments similar to those on page 18, the student, unless quite young, should fix in his mind or commit to memory the following or similar statements : —

Appearances of a Circle.

The eye is said to be in a plane, when if the plane were extended far enough, it would pass through the eye.

1. When the eye of the spectator is in the plane of a circle, its circumference will appear as a straight line.

2. When the line of direction is at right angles to the plane of a circle, its circumference will appear as the outline of a perfect circle.

3. When the line of direction is oblique to the plane of a circle, its circumference will appear as the circumference of an ellipse.

When the circumference of a circle appears as a straight line, or as the outline of a perfect circle, no special directions for drawing these forms are necessary beyond what are given for drawing them in general.

That appearance of the circle, however, which is most frequently seen, and therefore the most important of all, as well as the most difficult to execute, and the one to which we shall now give especial attention, is the ellipse.

Drawing The Ellipse.

An ellipse is a plane figure bounded by a curved line, from every point of which curve to two points within, called foci, the sum of the distances is the same.

The frequent and proper viewing and handling of circles, as directed in the explanations for the practical lessons in drawing them (see page 18), will be necessary in order to understand and apply the following : —

General Principles for Drawing Circles Represented by Ellipses.

1. Every ellipse has two axes or diameters, called a long diameter and a short diameter, which cross each other at their centers and at right angles; as A B and D E in Fig. 5.

2. When the eye of the spectator is in the plane of a circle and outside of its circumference, the short diameter of the ellipse appears as a point, and as the eye varies or departs from the A plane of the circle, the short diameter increases in apparent length until it may appear equal to the long diameter, which can only be true when the line of direction is at right angles to the plane of the circle.

3. The real center. of the ellipse and its long diameter do not coincide with the real center. and the diameter of the circle which it represents, being a little nearer • the eye of the spectator. In the diagram, Fig. 6, Pts. A B represents the long diameter of the ellipse, 1– 2 the diameter of the circle which the A 9 ellipse represents. This result is owing to the fact that the nearer half of a circle appears a little larger than the farther half.

4. When a circle is horizontal, its short diameter always appears vertical ; but when a circle is not horizontal, the apparent slant of the short diameter of the ellipse which represents it may always be found by joining with an imaginary line the nearest and the farthest points of the circle ; and the apparent slant of the long diameter will be at right angles to that of the short one.

Related Circles.

Circles may be related to one another in three ways :—

1. They may have the same axis ; that is their planes may be at right angles to the same straight line passing through their centers and at different distances from the eye of the spectator. See Fig. 7.

2. They may be in the same plane and at different distances from the eye of the spectator. B See Fig. 8.

3. They may be concentric ; that is, they may all have the same center. See Fig. 9.

Circles with the same Axis.

Proper experiments in viewing circles with the same axis will prove the following : —

When circles have the same axis, the one nearest the eye of the spectator appears foreshortened more than the others. In Fig. 7, the circles nearest the eye, whether above, below, left, or right of it, appear narrower in proportion to their length than those that are farther away.

Circles In the same Plane.

When circles are in the same plane, the one nearest the eye is foreshortened less than the others. In Fig. 8 the circles are supposed to be in the same plane ; hence the one nearest the eye appears wider in proportion to its length than the others that are farther away.
Concentric Circles.
When concentric circles in the same plane are viewed obliquely the following statements will be true : —

1. Their greatest apparent distance apart will beat the ends of the ellipses representing them See A— 1 and B— 2 in Fig. 9.
2. Their next greatest apparent distance will be at the point nearest the eye, as at D- 4 in Fig. 9.
3. Their least apparent distance will be at the point farthest from the eye. as at C - 3, in Fig. 9.
4. The greater the actual distance between the real sides, the greater will be the apparent distance between their long diameters. Notice the distance between and A- B in Fig. 9.